Graph
Graph:
A Graph is a non-linear data structure
It consists of a finite set of nodes (or vertices) and a set of edges connecting nodes.
A pair (x,y) is referred to as an edge, which communicates that the x vertex connects to the y vertex.
G=(V,E)
V={v1,v2,...............vn}
E={e1,e2,.............en}
Edge:
An edge connects two vertices.
Circles represent vertices, while lines represent edges.
Graphs are used to solve real-life problems that involve representation of the problem space as a network. Examples of networks include telephone networks, circuit networks, social networks (like LinkedIn, Facebook etc.).
For example, a single user in Facebook can be represented as a node (vertex) while their connection with others can be represented as an edge between nodes.
Each node can be a structure that contains information like user’s id, name, gender, etc.
Types of graphs:
Undirected Graph:
In an undirected graph, nodes are connected by edges that are all bidirectional. For example if an edge connects node 1 and 2, we can traverse from node 1 to node 2, and from node 2 to 1.
An undirected graph can have at most n(n-1)/2 edges.
Directed Graph
Sparse Graph
Dense graph
A dense graph is a graph in which the number of edges is close to the maximal number of edges.
Simple Graph
A graph with no loops and no parallel edges is called a simple graph.
The maximum number of edges possible in a single graph with 'n' vertices is nC2 where nC2 = n(n – 1)/2.
Degree of Vertex of a Graph
Degree of vertex can be considered under two cases of graphs −
- Undirected Graph
- Directed Graph
Degree of Vertex in an Undirected Graph
An undirected graph has no directed edges. Consider the following examples.
Example 1
Take a look at the following graph −
In the above Undirected Graph,
deg(a) = 2, as there are 2 edges meeting at vertex 'a'.
deg(b) = 3, as there are 3 edges meeting at vertex 'b'.
deg(c) = 1, as there is 1 edge formed at vertex 'c'
So 'c' is a pendent vertex.
deg(d) = 2, as there are 2 edges meeting at vertex 'd'.
deg(e) = 0, as there are 0 edges formed at vertex 'e'.
So 'e' is an isolated vertex.
Example 2
Take a look at the following graph −
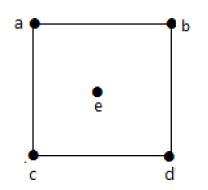
In the above graph,
deg(a) = 2, deg(b) = 2, deg(c) = 2, deg(d) = 2, and deg(e) = 0.
The vertex 'e' is an isolated vertex. The graph does not have any pendent vertex.
Indegree of a Graph
Indegree of vertex V is the number of edges which are coming into the vertex V.
Notation − deg−(V).
Outdegree of a Graph
Outdegree of vertex V is the number of edges which are going out from the vertex V.
Notation − deg+(V).
Consider the following examples.
Example 1
Take a look at the following directed graph. Vertex 'a' has two edges, 'ad' and 'ab', which are going outwards. Hence its outdegree is 2. Similarly, there is an edge 'ga', coming towards vertex 'a'. Hence the indegree of 'a' is 1.
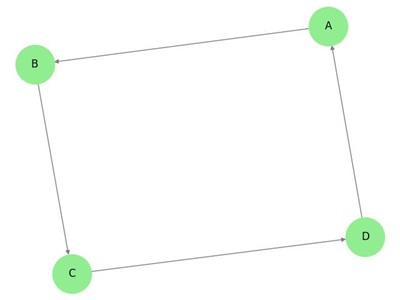
The indegree and outdegree of other vertices are shown in the following table −
| Vertex | Indegree | Outdegree |
|---|---|---|
| a | 1 | 2 |
| b | 2 | 0 |
| c | 2 | 1 |
| d | 1 | 1 |
| e | 1 | 1 |
| f | 1 | 1 |
| g | 0 | 2 |
Example 2
Take a look at the following directed graph. Vertex 'a' has an edge 'ae' going outwards from vertex 'a'. Hence its outdegree is 1. Similarly, the graph has an edge 'ba' coming towards vertex 'a'. Hence the indegree of 'a' is 1.
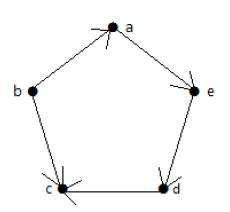
The indegree and outdegree of other vertices are shown in the following table −
| Vertex | Indegree | Outdegree |
|---|---|---|
| a | 1 | 1 |
| b | 0 | 2 |
| c | 2 | 0 |
| d | 1 | 1 |
| e | 1 | 1 |
Regular graph
a regular graph is a graph where each vertex has the same number of neighbors; i.e. every vertex has the same degree or valency
Eulerian Graph
A graph is considered Eulerian if the graph is both connected and has a closed trail (a walk with no repeated edges) containing all edges of the graph. Definition: An Eulerian Trail is a closed walk with no repeated edges but contains all edges of a graph and return to the start vertex.
The Seven Bridges of Königsberg
"Find a trail starting at one of the four islands (
Determining if a Graph is Eulerian
We will now look at criterion for determining if a graph is Eulerian with the following theorem.
| Theorem 1: A graph |
Consider the graph representing the Königsberg bridge problem. Notice that all vertices have odd degree:
| Vertex | Degree |
|---|---|




No comments:
Post a Comment