What is the result of the given postfix expression? abc*+ where a=1, b=2, c=3.
a) 4
b) 5
c) 6
d) 7
What is the result of the following postfix expression?
ab*cd*+ where a=2,b=2,c=3,d=4.
a) 16
b) 12
c) 14
d) 10
Evaluate the postfix expression ab + cd/- where a=5, b=4, c=9, d=3.
a) 23
b) 15
c) 6
d) 10
Evaluate and write the result for the following postfix expression
abc*+de*f+g*+ where a=1, b=2, c=3, d=4, e=5, f=6, g=2.
a) 61
b) 59
c) 60
d) 55
For the given expression tree, write the correct postfix expression.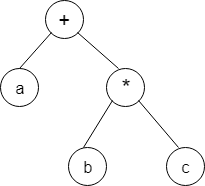
a) abc*+
b) abc+*
c) ab+c*
d) a+bc*
What would be the Prefix notation for the given equation?
A+(B*C)
a) +A*CB
b) *B+AC
c) +A*BC
d) *A+CB
What would be the Prefix notation for the given equation?
(A*B)+(C*D)
a) +*AB*CD
b) *+AB*CD
c) **AB+CD
d) +*BA*CD
What would be the Prefix notation for the given equation?
A+B*C^D
a) +A*B^CD
b) +A^B*CD
c) *A+B^CD
d) ^A*B+CD
What would be the Prefix notation for the given equation?
A^B^C^D
a) ^^^ABCD
b) ^A^B^CD
c) ABCD^^^
d) AB^C^D
What would be the Prefix notation for the given equation?
a+b-c/d&e|f
a) |&-+ab/cdef
b) &|-+ab/cdef
c) |&-ab+/cdef
d) |&-+/abcdef
What would be the Prefix notation for the given equation?
(a+(b/c)*(d^e)-f)
a) -+a*/^bcdef
b) -+a*/bc^def
c) -+a*b/c^def
d) -a+*/bc^def
What would be the Prefix notation and Postfix notation for the given equation?
A+B+C
a) ++ABC and AB+C+
b) AB+C+ and ++ABC
c) ABC++ and AB+C+
d) ABC+ and ABC+
What would be the Prefix notation for the given equation?
a|b&c
a) a|&bc
b) &|abc
c) |a&bc
d) ab&|c
What is the postfix expression for the corresponding infix expression?
a+b*c+(d*e)
a) abc*+de*+
b) abc+*de*+
c) a+bc*de+*
d) abc*+(de)*+
What is the postfix expression for the infix expression?
a-b-c
a) -ab-c
b) ab – c –
c) – -abc
d) -ab-c
What is the postfix expression for the following infix expression?
a/b^c-d
a) abc^/d-
b) ab/cd^-
c) ab/^cd-
d) abcd^/-
What is the corresponding postfix expression for the given infix expression?
a*(b+c)/d
a) ab*+cd/
b) ab+*cd/
c) abc*+/d
d) abc+*d/
What is the corresponding postfix expression for the given infix expression?
a+(b*c(d/e^f)*g)*h)
a) ab*cdef/^*g-h+
b) abcdef^/*g*h*+
c) abcd*^ed/g*-h*+
d) abc*de^fg/*-*h+
What is the correct postfix expression for the following expression?
a+b*(c^d-e)^(f+g*h)-i
a) abc^de-fg+*^*+i-
b) abcde^-fg*+*^h*+i-
c) abcd^e-fgh*+^*+i-
d) ab^-dc*+ef^gh*+i-
From the given Expression tree, identify the correct postfix expression from the list of options.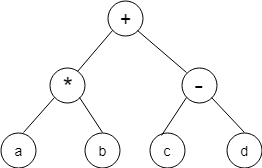
a) ab*cd*+
b) ab*cd-+
c) abcd-*+
d) ab*+cd-
What would be the solution to the given prefix notation?
- + 5 / 10 5 5
a) 2
b) 5
c) 10
d) 7
What would be the solution to the given prefix notation?
/ / / / 16 4 2 1
a) 1
b) 4
c) 2
d) 8
What would be the solution to the given prefix notation?
+ 9 * 3 / 8 4
a) 14
b) 15
c) 18
d) 12
What would be the solution to the given prefix notation?
- + 1 2 * 3 / 6 2
a) 6
b) -6
c) 3
d) -3
What would be the solution to the given prefix notation?
- * 1 5 / * / 6 3 6 2
a) 1
b) 0
c) -1
d) -2
What would be the solution to the given prefix notation?
* / + 1 2 / 4 2 + 3 5
a) 12
b) 7.5
c) 9
d) 13.5
The postfix expression abc+de/*- is equivalent to which of the following infix expression?
a) abc+-de*/
b) (a+b)-d/e*c
c) a-(b+c)*(d/e)
d) abc+*-(d/e)
The equivalent infix expression and value for the postfix form 1 2 + 3 * 4 5 * – will be ___________
a) 1 + 2 * 3 – 4 * 5 and -13
b) (2 + 1) * (3 – 4) * 5 and 13
c) 1 + 2 * (3 – 4) * 5 and -11
d) (1 + 2) * 3 – (4 * 5) and -11
What is the value of the postfix expression 2 3 + 4 5 6 – – *
a) 19
b) 21
c) -4
d) 25
The prefix expression of the postfix expression AB+CD-* is __________
a) (A+B)*(C-D)
b) +AB*-CD
c) A+*BCD-
d) *+AB-CD
Consider the postfix expression 4 5 6 a b 7 8 a c, where a, b, c are operators. Operator a has higher precedence over operators b and c. Operators b and c are right associative. Then, equivalent infix expression is
a) 4 a 5 6 b 7 8 a c
b) 4 a 5 c 6 b 7 a 8
c) 4 b 5 a 6 c 7 a 8
d) 4 a 5 b 6 c 7 a 8
The result of the postfix expression 5 3 * 9 + 6 / 8 4 / + is _____________
a) 8
b) 6
c) 10
d) 9


